Introduction to Boosting Algorithm
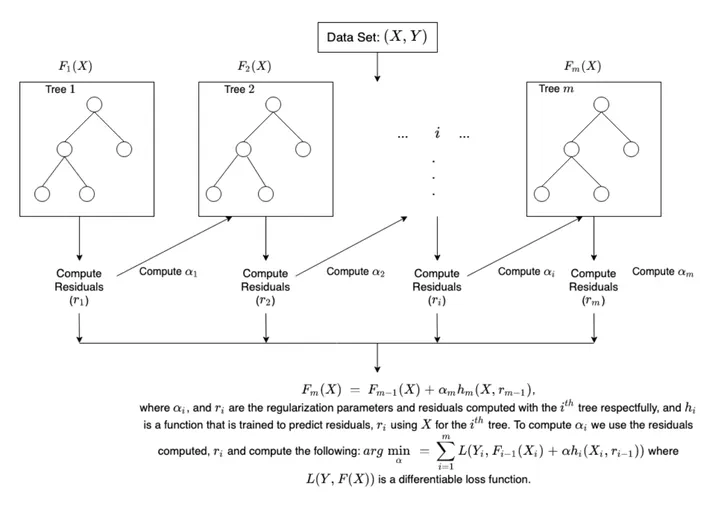
Overview
Boosting 是一种可将弱学习器提升为强学习器的算法,其理论依据是 Michael Kearns 和 Leslie Valiant 首先提出了”强可学习 (strongly learnable)”和“弱可学习 (weakly learnable)”的概念。他们指出:
一个概念(一个类,label),如果存在一个多项式的学习算法能够学习它,并且正确率很高,那么就称这个概念是强可学习的;
一个概念(一个类,label),如果存在一个多项式的学习算法能够学习它,学习的正确率仅比随机猜测略好,那么就称这个概念是弱可学习的。
Schapire后来证明了: 强可学习和弱可学习是等价的。 也就是说,在 PAC学习 (Probably Approximatly Correct Learning) 的框架下,“一个概念是强可学习的"的充分必要条件是“这个概念是弱可学习的”。 那么我们自然会思考:在学习中,如果已经发现了”弱学习算法”,那么能否将它提升为”强学习算法”呢?
Boosting的工作机制为:先从初始训练集训练出一个弱学习器,再根据弱学习器的表现对样本分布进行调整,使得先前的弱学习器识别错误的训练样本在后面的弱学习器中得到更多的关注(调高权重),然后基于调整后的样本分布来训练下一个基学习器;如此重复进行,直至基学习器数目达到指定的值,或整个集成算法结果达到退出条件,然后将这些学习器进行加权组合得到最终结果。 由前面过程可知 Boosting 是一个串行学习过程,后一个弱学习器的学习样本依赖于前一个弱学习器的学习结果。Boosting 模型较具代表性的算法有GBDT和AdaBoost等。在介绍这两种模型的原理之前,我们先思考两个问题:
前一个弱学习器在学习完后,怎么调整判断错误和判断正确样本的权重?
对于最终得到的多个弱学习器该怎么组合?即两个权重问题,一个是样本的权重怎么确定,另一个是弱学习器的权重怎么调整?对于任何一种Boosting算法,都需要解决这两个问题,而Boosting算法的核心也正在于这两个问题。
AdaBoost
AdaBoost (Adaptive Boosting) 是 Boosting 算法中的一个经典代表,由 Yoav Freund 和 Robert Schapire 在1995年提出。
分类问题
算法原理
对于分类问题,AdaBoost 首先从训练集用初始权重训练出一个弱学习器1 (只要比随机选择的效果好一些就行),这里的弱学习器可以为浅层决策树等算法,在 sklearn 的 AdaBoost.AdaBoostClassifier 中,默认的弱学习器就是深度为 $1$ 的决策树。然后根据弱学习器1的学习误差率来更新训练样本的权重并计算弱学习器1在最终组合时的权重,使得弱学习器1识别错误的的训练样本点的权重变高,从而使得这些识别错误的样本在后面的弱学习器2中得到更多的重视。基于调整权重后的训练集来训练弱学习器2(构建第二棵树),如此重复进行,直到弱学习器数达到事先指定的数目$T$,最终将这$T$个弱学习器通过加权组合策略进行整合,得到最终的强学习器。具体计算方法如下:
- 假设我们的训练集样本是一个二分类数据集:
在构建第一棵树(第一轮迭代)的时候每个样本的权重 $D_i(i)=\frac{1}{m}$.
- 第 k 个弱学习器在数据集上的加权错误率计算方法为:
其中
$$ I(G_k(x_i) \neq y_i) = \begin{cases} 1, & \text{if } G_k(x_i) \neq y_i, \\ 0, & \text{if } G_k(x_i) = y_i. \end{cases} $$实际上就是识别错误样本的权重和。例如在构建第一颗树的时候,如果有5个样本识别错误,则 $e_1=\frac{5}{m}$.
- 第 k 个弱学习器在最后组合为强学习器时的权重系数为:
可以发现:分类误差率 $e_k$ 越大,则对应的弱分类器权重系数 $\alpha_k$ 就越小,即在组合强分类器的时候越不重要。
- 假设第 k 个弱学习器学习的样本权重为 $D_k=(w_{k1}, w_{k2},\dots,w_{km})$,则第 k+1 个弱学习器第学习样本权重为:
可以发现:前一个弱学习器识别正确的样本权重变小了,识别错误的样本权重增大了。这里 $Z_K$ 是规范化因子:
$$ Z_k =\sum\limits_{i=1}^m w_{ki} \exp (-\alpha _k y_i G_k (x_i)) $$其实就是调整后的权重和,所以很容易得出调整后的样本权重和依然为1,这也解释了为什么在步骤 2 中计算错误率时,可以直接求和错误样本的权重得出。
- 最终的强分类器组合策略就很容易得出了:
损失函数
前向分布加法模型 (Forward Stagewise Additive Modeling)
如下式所示的便是一个加法模型:
$$f(x)=\sum\limits^M_{m=1}\beta_mb(x;\gamma_m)$$其中, $b(x;\gamma_m)$ 称为基函数, $\gamma_m$ 称为基函数的参数, $\beta_m$ 称为基函数的系数。Adaboost 算法其实是前向分步加法模型的特例, $b(x;\gamma_m)$ 相当于浅层决策树, $\beta_m$ 是弱学习器的权重, $\gamma_m$ 的弱学习器决策树的参数。
在给定训练数据及损失函数 $L(y,f(x))$ 的条件下,学习加法模型 $f(x)$ 的损失函数为:
$$\min\limits_{\beta_m,\gamma_m}\sum\limits^N_{i=1}L(y_i,\sum\limits^M_{m=1}\beta_mb(x_i;\gamma_m))$$其中, $M$ 是弱学习器的数量, $N$ 是学习样本集的数量。因为加法模型从前向后,每一步只学习一个基函数及其系数,且是学习前一个基学习器的错误部分,逐步逼近上式,则上式的损失函数可以简化如下,即每步只优化如下损失函数:
$$\min\limits_{\beta,\gamma}\sum\limits^N_{i=1}L(y_i,\beta b(x_i;\gamma))$$指数损失函数
在 Boosting 家族中,损失函数主要有以下几种:
| Name | Loss | Derivative | 目标函数 $f^*$ | Algorithm |
|---|---|---|---|---|
| Squared Error | $\frac{1}{2}(y^{(i)}-f(x^{(i)}))^2$ | $y^{(i)}-f(x^{(i)})$ | $E[y\vert x^{(i)}]$ | L2 Boosting |
| Absolute Error | $\lvert y^{(i)}-f(x^{(i)})\rvert$ | $sign(y^{(i)}-f(x^{(i)}))$ | $median(y\vert x^{(i)})$ | Gradient Boosting |
| Exponential Loss | $\exp(-y^{(i)}f(x^{(i)}))$ | $-y^{(i)}\exp(-y^{(i)}f(x^{(i)}))$ | $\frac{1}{2}\log\frac{\pi_i}{1-\pi_i}$ | Adaboost |
| Log Loss | $\log(1+e^{-y^{(i)}f(x^{(i)})})$ | $y^{(i)}-\pi_i$ | $\frac{1}{2}\log\frac{\pi_i}{1-\pi_i}$ | Logit Boost |
其中,Adaboost 使用的是指数损失函数。因为指数损失在分类问题上的效果要比均方误差更好,均方误差损失适合于输出是连续值的情况,
回归问题
算法原理
Adaboost 回归权重计算过程如下:
- 误差计算:对于第 k 个弱学习器,计算他在训练集的最大误差为
每个样本的相对误差为:
$$e_{ki}=\frac{\lvert y_i-G_k(x_i)\rvert}{E_k}$$实则是做归一化处理。这是误差损失为线性的情况。如果我们用平方误差,则
$$e_{ki}=\frac{(y_i-G_k(x_i))^2}{E_k^2}$$也可以用指数误差
$$e_{ki}=1-\exp(\frac{-\lvert y_i-G_k(x)\rvert}{E_k})$$则第 k 个弱学习器的加权误差率为:
$$e_k=\sum\limits^m_{i=1}w_{ki}e_{ki}$$- 弱学习器权重系数计算 $\alpha$ 计算:
- 样本权重更新公式为:
其中 $Z_k$ 为规范化因子
- 组合策略:取所有弱学习器预测结果的中位数,注意这里不同于分类问题的加权和方式。
GBDT (Gradient Boosting Decision Tree)
算法原理
不同于 Adaboost 通过调高识别错误样本的权重,从而不断纠正被学习错误的样本,GBDT 是通过不断学习前 k-1 个弱学习器组成的强学习器学习的残差(梯度提升),从而来弥补错误(区别于纠正)。这里可以发现 Adaboost 和 GBDT 一个很大的不同点,Adaboost 每一个弱学习器学习的样本标签是一样的,即假如某个样本的目标值(标签)是1,则每个弱学习训练过程的Y都是1,而GBDT每个弱学习器训练过程的Y却是不同的,学习的都是残差。
举个通俗理解的例子:假如有个人30岁,第一个弱学习器学习拟合后的值是20岁,残差是10岁,第二棵树去学习10这个目标,假如拟合的结果是8,残差是2,则第三棵树继续学习拟合2,依次进行下去。每一轮迭代,拟合的岁数误差都会减小,最后的拟合结果就是每个弱学习器的输出和。这里需要注意的一点是,GBDT 的弱学习器都是 CART 回归树,即使是分类问题,因为 GBDT 学习的梯度值是连续值。算法流程如下:
- 初始化弱学习器
M是样本数,$F_0(X)=G_0(X)$
- 对每个样本计算负梯度,即:
在 CART 回归树中,实则就是 $d_{mk}=y-c$,$c$ 是每个叶子节点样本标签的平均值。
将 2 中的残差作为样本新的目标值,并将 $(x_m,d_{mk})\quad m=1,2,\dots,M$作为下一棵树的训练数据。
基于 3 中新的训练数据,训练得到新的弱学习器,则新的强学习器为:
- 依次重复 2、3、4 步,直到达到指定的弱学习器个数或满足最低误差要求,最终的强学习器为:
正则化项
和 Adaboost 一样,GBDT 中也有正则化项,也就是学习率步长 $r$,这里用 $v$ 表示,最终的 GBDT 表达形式为:
$$F_k(X)=F_{k-1}(X)+v\times G_k(X)$$除了上面提到的正则化方法外,GBDT 还有另外一种通过控制采样方法进行正则化,和随机森林类似,但是 GBDT 是不放回采样。
分类问题
前面提到 GBDT 使用的弱学习器是 CART 回归树,即使是分类问题,但是因为类别直接加减是没有意义的,使用平方损失计算负梯度就没有意义,但是可以拟合分类类别的概率值,因为概率是连续值。但是对于多分类问题怎么得到每个类别的概率呢?结合我们深度学习处理多分类的经验,可以通过输出和类别数一样多的值,再通过$softmax$ 求概率。因此,在 GBDT 中,对于有 $k$ 个类别的分类任务 ($k>2$),如果迭代 $m$ 次,则共有 $k\times m$ 个 CART 树。
到这里,我们知道 GBDT 目标是拟合概率值,但不是直接去拟合概率值,而是去拟合类别标识 $y\in (-1,1)$。如果模型在类别 1 上的强学习器输出值比在其他类别上的强学习器输出大很多,那结果自然就是该类别,例如在类别 1 和 2 上的输出分别是 7 和 -0.5,这也是我们更希望看到的,因为差别越大,表示分类效果越好,所以下文实践部分我们会看到所有弱学习器的输出和会大于 1 或者小于 -1 很多,这都是正常的。这也从另一方面解释了为何在分类问题中我们选择对数似然损失函数,而不是平方损失函数。
为了解决损失计算问题,主要有两个方法,一个是用指数损失函数,此时 GBDT 退化为 Adaboost 算法。因为如果采用指数函数,那么 Adaboost 每一步就在拟合指数损失的梯度,根据在 Adaboost 部分介绍的指数损失函数的表达形式,也就是第t轮要学习的训练样本是 $(x_i,-y_i\exp(-y_if_{t-1}(x)))$,则全局损失为:
$$\begin{equation}\begin{aligned}\sum\limits^m_{i=1}Loss(f_{t-1}(x)+\alpha_tG_t(x),y_i) &=\sum\limits^m_{i=1}\exp(-y_i(f_{t-1}(x)+\alpha_tG_t(x))) \\ &=\sum\limits^m_{i=1}\exp(-y_if_{t-1}(x))\exp(-y_i\alpha_tG_t(x)) \\ &=\sum\limits^m_{i=1}w_{ti}^\prime\exp(-y_i\alpha G(x))\end{aligned}\end{equation}$$