Introduction to Kullback-Leibler Divergence

定义

假设对随机变量 $\xi$，存在两个概率分布 $P,Q$。如果为离散随机变量，定义从 $P$ 到 $Q$ 的 KL 散度为:

$$ \mathbb{D}_ {\text{KL}}(P\parallel Q)=\sum\limits_i P(i)\ln(\frac{P(i)}{Q(i)}) \tag{1.1} $$

如果 $\xi$ 为连续随机变量，则定义从 $P$ 到 $Q$ 的 KL 散度为:

$$ \mathbb{D}_ {\text{KL}}(P\parallel Q) =\int_{-\infty}^{\infty}p(\mathbf{x})\ln(\frac{p(\mathbf{x})}{q(\mathbf{x})})\text{d}\mathbf{x} \tag{1.2} $$

基本性质

以下叙述只讨论离散的情况。

非负性

$\mathbb{D}_{\text{KL}}(P\parallel Q)\geq0$，当且仅当 $P=Q$。

$proof:$

只需要证明 $\sum\limits_i P(i)\ln(\frac{Q(i)}{P(i)})\leq 0$。

利用不等式 $\ln(\mathbf{x})\leq\mathbf{x}-1,\forall x>0$，则：

$$ \begin{aligned} \sum\limits_i P(i)\ln(\frac{Q(i)}{P(i)}) & \leq \sum\limits_i P(i)(\frac{Q(i)}{P(i)}-1) \\ &=\sum\limits_i (Q(i)-P(i)) \\ &=0 \end{aligned} \tag{2.1.1} $$

取等号时当且仅当对于任意 $i$，$Q(i)=P(i)$ ，此时 $P=Q$。

上述不等式也被称为 Gibbs’ inequality：若 $\sum\limits_{i=1}^{n}p_i=\sum\limits_{i=1}^{n}q_i$ ，且 $p_i,q_i\in (0,1]$，则有

$$ -\sum\limits_{i=1}^{n}p_i\log p_i\leq -\sum\limits_{i=1}^{n}p_i\log q_i \tag{2.1.2} $$

等号成立当且仅当 $p_i=q_i\forall i$。

仿射变换不变性

假设 $\mathbf{y}=a\mathbf{x}+b$，那么： $\mathbb{D}_ {\text{KL}}(P(\mathbf{x})\parallel Q(\mathbf{x}))=\mathbb{D}_ {\text{KL}}(P(\mathbf{y})\parallel Q(\mathbf{y}))$

$proof:$

$$ \begin{aligned} \mathbb{D}_ {\text{KL}}(P(\mathbf{y})\parallel Q(\mathbf{y})) &=\int P(\mathbf{y})\log(\frac{P(\mathbf{y})}{Q(\mathbf{y})}) \\ &=\int P(\mathbf{x})\log(\frac{P(\mathbf{x})}{Q(\mathbf{x})}) \\ &=\mathbb{D}_{\text{KL}}(P(\mathbf{x})\parallel Q(\mathbf{x})) \end{aligned} \tag{2.2.1} $$

非对异性

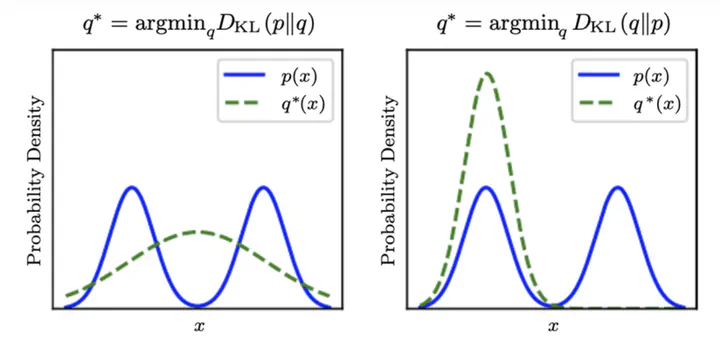
$\mathbb{D}_ {\text{KL}}(P\parallel Q)\neq \mathbb{D}_{\text{KL}}(Q\parallel P)$

值域

$\mathbb{D}_{\text{KL}}(P\parallel Q)$ 在一定条件下可以趋向于无穷。

从采样角度出发解释 KL 散度

KL 散度描述了我们用分布 $Q$ 来估计数据的真实分布 $P$ 的编码损失。

假设我们对于离散随机变量 $\xi$ 进行了 $n$ 次采样，并得到了 $\xi$ 取值的一组观测 $C=\{c_i\}$ ( $c_i$ 描述了随机变量 $\xi$ 取值为 $i$ 的次数)，记 $q_i$ 为分布 $Q$ 取值为 $i$ 的概率，即 $q_i=Q(i)$，那么观测 $C$ 由分布 $Q$ 生成的概率可以写成:

$$ \begin{aligned} L^n(c\vert Q) &=\left[\tbinom{n}{c_1}q_1^{c_1}\right] \left[\tbinom{n-c_1}{c_2}q_2^{c_2}\right]··· \left[\tbinom{n-c_1-···c_{k-1}}{c_k}q_k^{c_k}\right] \\ &=\frac{n!}{\prod\limits_ic_i!}\prod\limits_iq_i^{c_i} \end{aligned} \tag{3.1} $$

如果我们只观测一次，那么显然存在一个唯一的 $j$ 使得 $c_j=1$，而这种观测的由分布 $Q$ 生成的概率为 $q_j$，记作 $L^1(c\vert Q)=q_j$。

如果我们进行 $n+1$ 次观测，那么 $L^{n+1}(c\vert Q)$ 可以由第 $n$ 次观测所递推而来，即

$$ L^{n+1}(c\vert Q) = L^n(c\vert Q)\times\frac{n+1}{c_j+1}q_j \tag{3.2} $$

注意到 $\frac{n+1}{c_j+1}$ 服从伯努利大数定律，它将收敛到随机变量 $\xi$ 取值为 $j$ 的真实概率 $p_j$。

当我们进行无数次观测（即 $n\rightarrow \infty$），如果 $p_j = \lim\limits_ {n \rightarrow \infty} \frac{c_j+1}{n+1} \rightarrow q_j$，那么 $L^n$ 会收敛($n\rightarrow \infty$)，此时代表分布 $Q$ 可以很好估计真实分布 $P$，而其它情况则可能会发散。

为了描述进行一次观测的平均概率，我们对 $n$ 次观测采用几何平均数，记作 $\bar{L}$:

$$ \bar{L}=(L^n(c\vert Q))^{\frac{1}{n}}=(\frac{n!}{\prod\limits_ic_i!})^{\frac{1}{n}}\prod\limits_iq_i^{\frac{c_i}{n}} \tag{3.3} $$

用 $P$ 来描述 $\xi$ 的真实分布，如果 $\frac{c_i}{n} \rightarrow p_i = q_i $，那么 $n\rightarrow \infty$ ， $\bar{L}\rightarrow 1$ 。如果 $p_i\neq q_i$ ，那么 $\bar{L}$ 则可能不会收敛。令 $n\rightarrow \infty$ ，此时我们有:

$$ \log_{2}(\overline{L}) =\frac{1}{n}(\log n! -\sum\limits_{i}\log c_{i}!) +\sum\limits_{i}p_{i}\log q_{i} \tag{3.4} $$

当 $n\rightarrow \infty$ 时，由 $\frac{c_i}{n}\rightarrow p_i>0$，可知 $c_i\rightarrow \infty$。

又当 $n\rightarrow \infty,c_i\rightarrow \infty$ 时，有极限：

$$ \begin{aligned} \log n! &\rightarrow n\log n-n \\ \log c_i! &\rightarrow c_i\log c_i-c_i \end{aligned} $$

我们可以将式 $(3.4)$ 重写为:

$$ \begin{aligned} \log_2(\bar{L}) &= \frac{(n \log n - n) - \sum\limits_i (c_i \log c_i - c_i) + n\sum\limits_i p_i \log q_i}{n} \\ &= \log n - 1 - \frac{1}{n} \sum_i (c_i \log c_i - c_i) + \sum_i p_i \log q_i \end{aligned} \tag{3.5} $$

注意到：

$$ \begin{aligned} \log(n) &= \sum\limits_i\frac{c_i}{n}\log(n) \\ \sum\limits_i \frac{c_i}{n} &= 1 \\ \frac{c_i}{n} &\rightarrow p_i \end{aligned} $$

因此我们可以将式 $(3.5)$ 简化为:

$$ \begin{aligned} \log_2(\bar{L}) &= \sum_i \frac{c_i}{n} \log(n) - \sum_i \frac{c_i}{n} \log(c_i) + \sum_i p_i \log(q_i) \\ &= \sum_i \left[ p_i \log(n) - p_i \log(c_i) + p_i \log(q_i) \right] \\ &= \sum_i \left[ -p_i \log(p_i) + p_i \log(q_i) \right] \\ &= -D_{KL}(P \parallel Q) \end{aligned} \tag{3.6} $$

综上所述，当 $P,Q$ 两个分布的概率密度函数几乎处处相等的时候，有 $\bar{L}=1$ ，由式 $(2.6)$ 可知 $\mathbb{D}_ {KL}=0$ ；当两个分布相差太大的时候，有 $\bar{L}\rightarrow 0$ ，可知 $\mathbb{D}_ {KL}=\infty$ 。KL 散度度量了在对随机变量 $\xi$ 的采样过程中， $\xi$ 的真实分布 $P$ 与我们的假设分布 $Q$ 的符合程度。

KL散度的应用：独立性度量

我们可以用 KL 散度来度量两个随机变量 $\mathbf{x},\mathbf{y}$ 的独立性：

$$ \begin{aligned} I(\mathbf{x}; \mathbf{y}) &= D_{KL}(P = P(\mathbf{x}, \mathbf{y}) \parallel Q = P(\mathbf{x})P(\mathbf{y})) \\ &= \sum_{x,y} p(\mathbf{x}, \mathbf{y}) \ln \left( \frac{p(\mathbf{x}, \mathbf{y})}{p(\mathbf{x})p(\mathbf{y})} \right) \end{aligned} \tag{4.1} $$

如果 $\mathbf{x},\mathbf{y}$ 统计独立，那么 $I(\mathbf{x};\mathbf{y})=0$。 同时，在信息论的角度，定义随机变量的交叉熵为:

$$ H[x] = - \sum\limits_x p(x) \ln p(x) $$

推导可知：

$$ \begin{aligned} H[x|y] &= - \int p(y) \int p(x|y) \ln p(x|y) \, \text{d}x \, \text{d}y \\ H[y|x] &= - \int p(x) \int p(y|x) \ln p(y|x) \, \text{d}y \, \text{d}x \end{aligned} $$

此时有：

$$ \begin{aligned} I(\mathbf{x}, \mathbf{y}) &= - \int \int p(\mathbf{x}, \mathbf{y}) \ln \left (\frac{p(\mathbf{x})p(\mathbf{y})}{p(\mathbf{x}, \mathbf{y})} \right) \text{d}\mathbf{x}\text{d}\mathbf{y} \\ &= - \int \int p(\mathbf{x}, \mathbf{y}) \ln(p(\mathbf{x})) \text{d}\mathbf{x}\text{d}\mathbf{y} + \int \int p(\mathbf{x}, \mathbf{y}) \ln(p(\mathbf{x}\vert\mathbf{y})) \text{d}\mathbf{x}\text{d}\mathbf{y} \\ &= - \int \left[\int p(\mathbf{x}, \mathbf{y})\text{d}\mathbf{y}\right] \ln(p(\mathbf{x})) \text{d}\mathbf{x} + \int \int \left[p(\mathbf{x}\vert \mathbf{y})p(y) \right] \ln(p(\mathbf{x}\vert \mathbf{y})) \text{d}\mathbf{x}\text{d}\mathbf{y} \\ &= - \int p(x) \ln(p(\mathbf{x})) \text{d}\mathbf{x} + \int p(y)\int p(\mathbf{x}\vert \mathbf{y}) \ln(p(\mathbf{x}\vert \mathbf{y})) \text{d}\mathbf{x}\text{d}\mathbf{y} \\ &= H[\mathbf{x}] - H[\mathbf{x}\vert\mathbf{y}] \end{aligned} \tag{4.2} $$

同理有：

$$ I(\mathbf{x}, \mathbf{y})= H[\mathbf{y}] - H[\mathbf{y}\vert\mathbf{x}] \tag{4.3} $$

两个多元正态分布的 KL 散度

假设 $x=(\mathbf{x}_1,\mathbf{x}_2,···,\mathbf{x}_n)$ 为多元正态分布随机向量，且

$$ \begin{aligned} P_1(\mathbf{x}) &= \frac{1}{(2\pi)^{\frac{n}{2}} \det(\Sigma_1)^{\frac{1}{2}}} \exp\left(-\frac{1}{2} (\mathbf{x} - \mathbf{u}_1)^T \Sigma_1^{-1} (\mathbf{x} - \mathbf{u}_1)\right) \\ P_2(\mathbf{x}) &= \frac{1}{(2\pi)^{\frac{n}{2}} \det(\Sigma_2)^{\frac{1}{2}}} \exp\left(-\frac{1}{2} (\mathbf{x} - \mathbf{u}_2)^T \Sigma_2^{-1} (\mathbf{x} - \mathbf{u}_2)\right) \end{aligned} $$

那么可以证明

$$ D(P_1\parallel P_2)=\frac{1}{2}\left[\log\frac{\det(\Sigma_2)}{\det(\Sigma_1)}+\mathrm{Tr}(\Sigma_2^{-1}\Sigma_1)+(u_1-u_2)^T\Sigma_2^{-1}(u_1-u_2)-n\right] $$

$proof:$

$$ \begin{aligned} D(P_1\parallel P_2) &= \sum\limits_i P_1(i)\log\frac{P_1(i)}{P_2(i)} \\ &= E_{P_1}\left(\log P_1-\log P_2\right) \\ &= \frac{1}{2} E_{P_1}\left[ - \log\det (\Sigma_ 1) + \log\det (\Sigma_ 2) - (\mathbf{x} - \mathbf{u}_ 1)^ T \Sigma_ 1^ {-1} (\mathbf{x} - \mathbf{u}_ 1) + (\mathbf{x} - \mathbf{u}_ 2)^ T \Sigma_ 2^{-1} (\mathbf{x} - \mathbf{u}_2)\right] \\ &= \frac{1}{2}\log\frac{\det(\Sigma_2)}{\det(\Sigma_1)}+\frac{1}{2}E_{P_1}\left[(\mathbf{x} - \mathbf{u}_2)^T \Sigma_2^{-1} (\mathbf{x} - \mathbf{u}_2)-(\mathbf{x} - \mathbf{u}_1)^T \Sigma_1^{-1} (\mathbf{x} - \mathbf{u}_1)\right] \\ &= \frac{1}{2}\log\frac{\det(\Sigma_2)}{\det(\Sigma_1)}+\frac{1}{2}E_{P_1}\left[\text{Tr}((\mathbf{x} - \mathbf{u}_2)^T \Sigma_2^{-1} (\mathbf{x} - \mathbf{u}_2))-\text{Tr}((\mathbf{x} - \mathbf{u}_1)^T \Sigma_1^{-1} (\mathbf{x} - \mathbf{u}_1))\right] \\ &= \frac{1}{2}\log\frac{\det(\Sigma_2)}{\det(\Sigma_1)}+\frac{1}{2}E_{P_1}\left[\text{Tr}(\Sigma_2^{-1} (\mathbf{x} - \mathbf{u}_2)(\mathbf{x} - \mathbf{u}_2)^T )-\text{Tr}(\Sigma_1^{-1} (\mathbf{x} - \mathbf{u}_1)(\mathbf{x} - \mathbf{u}_1)^T )\right] \end{aligned} \tag{5.1} $$

当 $P_1,P_2$ 不为同分布时，由于 $\mathbf{x}$ 服从 $P_1$ 分布，可知

$$ \begin{aligned} (\mathbf{x} - \mathbf{u}_1)(\mathbf{x} - \mathbf{u}_1)^T = \Sigma_1 \\ (\mathbf{x} - \mathbf{u}_2)(\mathbf{x} - \mathbf{u}_2)^T \neq \Sigma_2 \end{aligned} $$

故式 $(5.1)$ 可化简为:

$$ \begin{aligned} D(P_1\parallel P_2) &= \frac{1}{2}\log\frac{\det(\Sigma_2)}{\det(\Sigma_1)}+\frac{1}{2}E_{P_1}\left[\text{Tr}(\Sigma_2^{-1} (\mathbf{x} - \mathbf{u}_2)(\mathbf{x} - \mathbf{u}_2)^T)-1\right] \\ &= \frac{1}{2}\log\frac{\det(\Sigma_2)}{\det(\Sigma_1)}+\frac{1}{2}E_{P_1}\left[\text{Tr}(\Sigma_2^{-1} (\mathbf{x} - \mathbf{u}_1+(\mathbf{u}_1-\mathbf{u}_2))(\mathbf{x} - \mathbf{u}_1+(\mathbf{u}_1-\mathbf{u}_2))^T)-1\right] \\ &= \frac{1}{2}\log\frac{\det(\Sigma_2)}{\det(\Sigma_1)}+\frac{1}{2}\mathbb{E}_{P_1} \left[ \text{Tr}\left(\Sigma_2^{-1} \left( \Sigma_1 + 2 (\mathbf{x} - \mathbf{u}_1)(\mathbf{u}_1 - \mathbf{u}_2)^{\top} + (\mathbf{u}_1 - \mathbf{u}_2)(\mathbf{u}_1 - \mathbf{u}_2)^{\top} \right) \right) \right] \\ &= \frac{1}{2}\left[\log\frac{\det(\Sigma_2)}{\det(\Sigma_1)} + \text{Tr}(\Sigma_2^{-1} \Sigma_1) + (\mathbf{u}_1 - \mathbf{u}_2)^{\top} \Sigma_2^{-1} (\mathbf{u}_1 - \mathbf{u}_2) - n\right] \end{aligned} \tag{5.2} $$